ਜਦੋਂ ਗੱਲ ਆਉਂਦੀ ਹੈਐਂਟੀਨਾ, ਜਿਸ ਸਵਾਲ ਬਾਰੇ ਲੋਕ ਸਭ ਤੋਂ ਵੱਧ ਚਿੰਤਤ ਹਨ ਉਹ ਹੈ "ਰੇਡੀਏਸ਼ਨ ਅਸਲ ਵਿੱਚ ਕਿਵੇਂ ਪ੍ਰਾਪਤ ਕੀਤੀ ਜਾਂਦੀ ਹੈ?" ਸਿਗਨਲ ਸਰੋਤ ਦੁਆਰਾ ਪੈਦਾ ਕੀਤਾ ਗਿਆ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਖੇਤਰ ਟ੍ਰਾਂਸਮਿਸ਼ਨ ਲਾਈਨ ਰਾਹੀਂ ਅਤੇ ਐਂਟੀਨਾ ਦੇ ਅੰਦਰ ਕਿਵੇਂ ਫੈਲਦਾ ਹੈ, ਅਤੇ ਅੰਤ ਵਿੱਚ ਐਂਟੀਨਾ ਤੋਂ "ਅਲੱਗ" ਹੋ ਕੇ ਇੱਕ ਖਾਲੀ ਸਪੇਸ ਵੇਵ ਬਣਾਉਂਦਾ ਹੈ।
1. ਸਿੰਗਲ ਵਾਇਰ ਰੇਡੀਏਸ਼ਨ
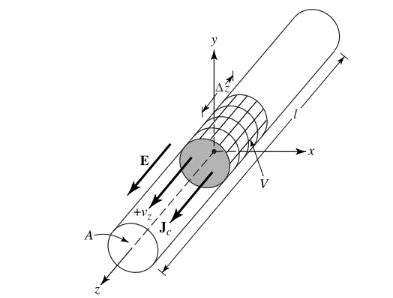
ਮੰਨ ਲਓ ਕਿ ਚਾਰਜ ਘਣਤਾ, ਜਿਸਨੂੰ qv (Coulomb/m3) ਵਜੋਂ ਦਰਸਾਇਆ ਗਿਆ ਹੈ, ਇੱਕ ਗੋਲਾਕਾਰ ਤਾਰ ਵਿੱਚ ਇੱਕਸਾਰ ਵੰਡਿਆ ਹੋਇਆ ਹੈ ਜਿਸਦਾ ਕਰਾਸ-ਸੈਕਸ਼ਨਲ ਖੇਤਰ a ਅਤੇ ਆਇਤਨ V ਹੈ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ 1 ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ।
ਚਿੱਤਰ 1
ਆਇਤਨ V ਵਿੱਚ ਕੁੱਲ ਚਾਰਜ Q ਇੱਕ ਸਮਾਨ ਗਤੀ Vz (m/s) ਨਾਲ z ਦਿਸ਼ਾ ਵਿੱਚ ਚਲਦਾ ਹੈ। ਇਹ ਸਾਬਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਤਾਰ ਦੇ ਕਰਾਸ ਸੈਕਸ਼ਨ 'ਤੇ ਮੌਜੂਦਾ ਘਣਤਾ Jz ਹੈ:
Jz = qv vz (1)
ਜੇਕਰ ਤਾਰ ਇੱਕ ਆਦਰਸ਼ ਕੰਡਕਟਰ ਤੋਂ ਬਣੀ ਹੈ, ਤਾਂ ਤਾਰ ਦੀ ਸਤ੍ਹਾ 'ਤੇ ਮੌਜੂਦਾ ਘਣਤਾ Js ਹੈ:
ਜੇਐਸ = ਕਿਊਐਸ ਵੀਜ਼ੈਡ (2)
ਜਿੱਥੇ qs ਸਤਹ ਚਾਰਜ ਘਣਤਾ ਹੈ। ਜੇਕਰ ਤਾਰ ਬਹੁਤ ਪਤਲੀ ਹੈ (ਆਦਰਸ਼ਕ ਤੌਰ 'ਤੇ, ਰੇਡੀਅਸ 0 ਹੈ), ਤਾਂ ਤਾਰ ਵਿੱਚ ਕਰੰਟ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ:
Iz = ql vz (3)
ਜਿੱਥੇ ql (ਕੂਲੰਬ/ਮੀਟਰ) ਪ੍ਰਤੀ ਯੂਨਿਟ ਲੰਬਾਈ ਦਾ ਚਾਰਜ ਹੈ।
ਅਸੀਂ ਮੁੱਖ ਤੌਰ 'ਤੇ ਪਤਲੀਆਂ ਤਾਰਾਂ ਨਾਲ ਸਬੰਧਤ ਹਾਂ, ਅਤੇ ਸਿੱਟੇ ਉਪਰੋਕਤ ਤਿੰਨਾਂ ਮਾਮਲਿਆਂ 'ਤੇ ਲਾਗੂ ਹੁੰਦੇ ਹਨ। ਜੇਕਰ ਕਰੰਟ ਸਮੇਂ-ਬਦਲਦਾ ਹੈ, ਤਾਂ ਸਮੇਂ ਦੇ ਸੰਬੰਧ ਵਿੱਚ ਫਾਰਮੂਲਾ (3) ਦਾ ਡੈਰੀਵੇਟਿਵ ਇਸ ਪ੍ਰਕਾਰ ਹੈ:
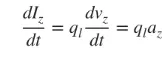
(4)
az ਚਾਰਜ ਪ੍ਰਵੇਗ ਹੈ। ਜੇਕਰ ਤਾਰ ਦੀ ਲੰਬਾਈ l ਹੈ, ਤਾਂ (4) ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਲਿਖਿਆ ਜਾ ਸਕਦਾ ਹੈ:
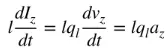
(5)
ਸਮੀਕਰਨ (5) ਕਰੰਟ ਅਤੇ ਚਾਰਜ ਵਿਚਕਾਰ ਮੂਲ ਸਬੰਧ ਹੈ, ਅਤੇ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਰੇਡੀਏਸ਼ਨ ਦਾ ਵੀ ਮੂਲ ਸਬੰਧ ਹੈ। ਸਿੱਧੇ ਸ਼ਬਦਾਂ ਵਿੱਚ, ਰੇਡੀਏਸ਼ਨ ਪੈਦਾ ਕਰਨ ਲਈ, ਚਾਰਜ ਦਾ ਸਮਾਂ-ਬਦਲਦਾ ਕਰੰਟ ਜਾਂ ਪ੍ਰਵੇਗ (ਜਾਂ ਗਿਰਾਵਟ) ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ। ਅਸੀਂ ਆਮ ਤੌਰ 'ਤੇ ਸਮਾਂ-ਹਾਰਮੋਨਿਕ ਐਪਲੀਕੇਸ਼ਨਾਂ ਵਿੱਚ ਕਰੰਟ ਦਾ ਜ਼ਿਕਰ ਕਰਦੇ ਹਾਂ, ਅਤੇ ਚਾਰਜ ਦਾ ਜ਼ਿਕਰ ਅਕਸਰ ਅਸਥਾਈ ਐਪਲੀਕੇਸ਼ਨਾਂ ਵਿੱਚ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਚਾਰਜ ਪ੍ਰਵੇਗ (ਜਾਂ ਗਿਰਾਵਟ) ਪੈਦਾ ਕਰਨ ਲਈ, ਤਾਰ ਨੂੰ ਮੋੜਿਆ, ਮੋੜਿਆ ਅਤੇ ਅਸੰਬੰਧਿਤ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ। ਜਦੋਂ ਚਾਰਜ ਸਮਾਂ-ਹਾਰਮੋਨਿਕ ਗਤੀ ਵਿੱਚ ਘੁੰਮਦਾ ਹੈ, ਤਾਂ ਇਹ ਸਮੇਂ-ਸਮੇਂ 'ਤੇ ਚਾਰਜ ਪ੍ਰਵੇਗ (ਜਾਂ ਗਿਰਾਵਟ) ਜਾਂ ਸਮਾਂ-ਬਦਲਦਾ ਕਰੰਟ ਵੀ ਪੈਦਾ ਕਰੇਗਾ। ਇਸ ਲਈ:
1) ਜੇਕਰ ਚਾਰਜ ਹਿੱਲਦਾ ਨਹੀਂ ਹੈ, ਤਾਂ ਕੋਈ ਕਰੰਟ ਨਹੀਂ ਹੋਵੇਗਾ ਅਤੇ ਨਾ ਹੀ ਕੋਈ ਰੇਡੀਏਸ਼ਨ ਹੋਵੇਗਾ।
2) ਜੇਕਰ ਚਾਰਜ ਇੱਕ ਸਥਿਰ ਗਤੀ ਨਾਲ ਚਲਦਾ ਹੈ:
a. ਜੇਕਰ ਤਾਰ ਸਿੱਧੀ ਅਤੇ ਅਨੰਤ ਲੰਬਾਈ ਵਾਲੀ ਹੋਵੇ, ਤਾਂ ਕੋਈ ਰੇਡੀਏਸ਼ਨ ਨਹੀਂ ਹੁੰਦੀ।
b. ਜੇਕਰ ਤਾਰ ਮੁੜੀ ਹੋਈ, ਮੁੜੀ ਹੋਈ, ਜਾਂ ਟੁੱਟੀ ਹੋਈ ਹੈ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ 2 ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ, ਤਾਂ ਰੇਡੀਏਸ਼ਨ ਹੁੰਦੀ ਹੈ।
3) ਜੇਕਰ ਚਾਰਜ ਸਮੇਂ ਦੇ ਨਾਲ ਘੁੰਮਦਾ ਰਹਿੰਦਾ ਹੈ, ਤਾਂ ਚਾਰਜ ਰੇਡੀਏਟ ਕਰੇਗਾ ਭਾਵੇਂ ਤਾਰ ਸਿੱਧੀ ਹੋਵੇ।
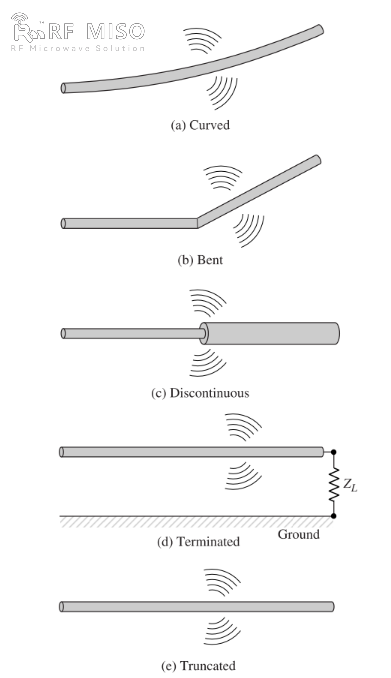
ਚਿੱਤਰ 2
ਰੇਡੀਏਸ਼ਨ ਵਿਧੀ ਦੀ ਗੁਣਾਤਮਕ ਸਮਝ ਇੱਕ ਖੁੱਲ੍ਹੀ ਤਾਰ ਨਾਲ ਜੁੜੇ ਇੱਕ ਪਲਸਡ ਸਰੋਤ ਨੂੰ ਦੇਖ ਕੇ ਪ੍ਰਾਪਤ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ਜਿਸਨੂੰ ਇਸਦੇ ਖੁੱਲ੍ਹੇ ਸਿਰੇ 'ਤੇ ਇੱਕ ਲੋਡ ਰਾਹੀਂ ਜ਼ਮੀਨ 'ਤੇ ਰੱਖਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ 2(d) ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ। ਜਦੋਂ ਤਾਰ ਨੂੰ ਸ਼ੁਰੂ ਵਿੱਚ ਊਰਜਾ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ, ਤਾਂ ਤਾਰ ਵਿੱਚ ਚਾਰਜ (ਮੁਫ਼ਤ ਇਲੈਕਟ੍ਰੌਨ) ਸਰੋਤ ਦੁਆਰਾ ਤਿਆਰ ਕੀਤੀਆਂ ਗਈਆਂ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ ਦੁਆਰਾ ਗਤੀ ਵਿੱਚ ਸੈੱਟ ਕੀਤੇ ਜਾਂਦੇ ਹਨ। ਜਿਵੇਂ ਕਿ ਚਾਰਜ ਤਾਰ ਦੇ ਸਰੋਤ ਸਿਰੇ 'ਤੇ ਤੇਜ਼ ਹੁੰਦੇ ਹਨ ਅਤੇ ਜਦੋਂ ਇਸਦੇ ਸਿਰੇ 'ਤੇ ਪ੍ਰਤੀਬਿੰਬਤ ਹੁੰਦੇ ਹਨ ਤਾਂ ਹੌਲੀ ਹੋ ਜਾਂਦੇ ਹਨ (ਮੂਲ ਗਤੀ ਦੇ ਮੁਕਾਬਲੇ ਨਕਾਰਾਤਮਕ ਪ੍ਰਵੇਗ), ਇਸਦੇ ਸਿਰਿਆਂ 'ਤੇ ਅਤੇ ਬਾਕੀ ਤਾਰ ਦੇ ਨਾਲ ਇੱਕ ਰੇਡੀਏਸ਼ਨ ਖੇਤਰ ਪੈਦਾ ਹੁੰਦਾ ਹੈ। ਚਾਰਜਾਂ ਦਾ ਪ੍ਰਵੇਗ ਬਲ ਦੇ ਇੱਕ ਬਾਹਰੀ ਸਰੋਤ ਦੁਆਰਾ ਪੂਰਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਜੋ ਚਾਰਜਾਂ ਨੂੰ ਗਤੀ ਵਿੱਚ ਸੈੱਟ ਕਰਦਾ ਹੈ ਅਤੇ ਸੰਬੰਧਿਤ ਰੇਡੀਏਸ਼ਨ ਖੇਤਰ ਪੈਦਾ ਕਰਦਾ ਹੈ। ਤਾਰ ਦੇ ਸਿਰਿਆਂ 'ਤੇ ਚਾਰਜਾਂ ਦਾ ਘਟਣਾ ਪ੍ਰੇਰਿਤ ਖੇਤਰ ਨਾਲ ਜੁੜੇ ਅੰਦਰੂਨੀ ਬਲਾਂ ਦੁਆਰਾ ਪੂਰਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਜੋ ਕਿ ਤਾਰ ਦੇ ਸਿਰਿਆਂ 'ਤੇ ਕੇਂਦਰਿਤ ਚਾਰਜਾਂ ਦੇ ਇਕੱਠੇ ਹੋਣ ਕਾਰਨ ਹੁੰਦਾ ਹੈ। ਅੰਦਰੂਨੀ ਬਲ ਚਾਰਜ ਦੇ ਇਕੱਠੇ ਹੋਣ ਤੋਂ ਊਰਜਾ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਨ ਕਿਉਂਕਿ ਇਸਦਾ ਵੇਗ ਤਾਰ ਦੇ ਸਿਰਿਆਂ 'ਤੇ ਜ਼ੀਰੋ ਹੋ ਜਾਂਦਾ ਹੈ। ਇਸ ਲਈ, ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਐਕਸਾਈਟੇਸ਼ਨ ਕਾਰਨ ਚਾਰਜਾਂ ਦਾ ਪ੍ਰਵੇਗ ਅਤੇ ਵਾਇਰ ਇਮਪੀਡੈਂਸ ਦੀ ਡਿਸਕੰਟੀਨਿਊਟੀ ਜਾਂ ਸੁਚਾਰੂ ਵਕਰ ਕਾਰਨ ਚਾਰਜਾਂ ਦਾ ਘਟਣਾ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਰੇਡੀਏਸ਼ਨ ਪੈਦਾ ਕਰਨ ਲਈ ਵਿਧੀਆਂ ਹਨ। ਹਾਲਾਂਕਿ ਮੈਕਸਵੈੱਲ ਦੇ ਸਮੀਕਰਨਾਂ ਵਿੱਚ ਮੌਜੂਦਾ ਘਣਤਾ (Jc) ਅਤੇ ਚਾਰਜ ਘਣਤਾ (qv) ਦੋਵੇਂ ਸਰੋਤ ਸ਼ਬਦ ਹਨ, ਚਾਰਜ ਨੂੰ ਇੱਕ ਵਧੇਰੇ ਬੁਨਿਆਦੀ ਮਾਤਰਾ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ, ਖਾਸ ਕਰਕੇ ਅਸਥਾਈ ਖੇਤਰਾਂ ਲਈ। ਹਾਲਾਂਕਿ ਰੇਡੀਏਸ਼ਨ ਦੀ ਇਹ ਵਿਆਖਿਆ ਮੁੱਖ ਤੌਰ 'ਤੇ ਅਸਥਾਈ ਅਵਸਥਾਵਾਂ ਲਈ ਵਰਤੀ ਜਾਂਦੀ ਹੈ, ਇਸਦੀ ਵਰਤੋਂ ਸਥਿਰ-ਅਵਸਥਾ ਰੇਡੀਏਸ਼ਨ ਦੀ ਵਿਆਖਿਆ ਕਰਨ ਲਈ ਵੀ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ।
ਕਈ ਸ਼ਾਨਦਾਰ ਸਿਫ਼ਾਰਸ਼ ਕਰੋਐਂਟੀਨਾ ਉਤਪਾਦਦੁਆਰਾ ਨਿਰਮਿਤਆਰ.ਐਫ.ਐਮ.ਐਸ.ਓ.:
2. ਦੋ-ਤਾਰ ਰੇਡੀਏਸ਼ਨ
ਇੱਕ ਵੋਲਟੇਜ ਸਰੋਤ ਨੂੰ ਇੱਕ ਐਂਟੀਨਾ ਨਾਲ ਜੁੜੀ ਦੋ-ਕੰਡਕਟਰ ਟ੍ਰਾਂਸਮਿਸ਼ਨ ਲਾਈਨ ਨਾਲ ਜੋੜੋ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ 3(a) ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ। ਦੋ-ਤਾਰ ਲਾਈਨ 'ਤੇ ਵੋਲਟੇਜ ਲਗਾਉਣ ਨਾਲ ਕੰਡਕਟਰਾਂ ਵਿਚਕਾਰ ਇੱਕ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਪੈਦਾ ਹੁੰਦੀ ਹੈ। ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ ਹਰੇਕ ਕੰਡਕਟਰ ਨਾਲ ਜੁੜੇ ਮੁਕਤ ਇਲੈਕਟ੍ਰੌਨਾਂ (ਪਰਮਾਣੂਆਂ ਤੋਂ ਆਸਾਨੀ ਨਾਲ ਵੱਖ) 'ਤੇ ਕੰਮ ਕਰਦੀਆਂ ਹਨ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਹਿੱਲਣ ਲਈ ਮਜਬੂਰ ਕਰਦੀਆਂ ਹਨ। ਚਾਰਜਾਂ ਦੀ ਗਤੀ ਕਰੰਟ ਪੈਦਾ ਕਰਦੀ ਹੈ, ਜੋ ਬਦਲੇ ਵਿੱਚ ਇੱਕ ਚੁੰਬਕੀ ਖੇਤਰ ਪੈਦਾ ਕਰਦੀ ਹੈ।
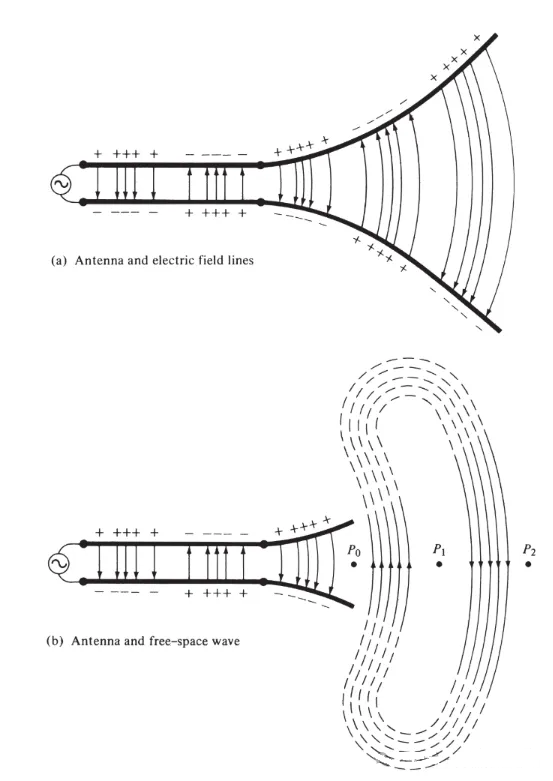
ਚਿੱਤਰ 3
ਅਸੀਂ ਸਵੀਕਾਰ ਕੀਤਾ ਹੈ ਕਿ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ ਸਕਾਰਾਤਮਕ ਚਾਰਜਾਂ ਨਾਲ ਸ਼ੁਰੂ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਨੈਗੇਟਿਵ ਚਾਰਜਾਂ ਨਾਲ ਖਤਮ ਹੁੰਦੀਆਂ ਹਨ। ਬੇਸ਼ੱਕ, ਉਹ ਸਕਾਰਾਤਮਕ ਚਾਰਜਾਂ ਨਾਲ ਵੀ ਸ਼ੁਰੂ ਹੋ ਸਕਦੀਆਂ ਹਨ ਅਤੇ ਅਨੰਤਤਾ 'ਤੇ ਖਤਮ ਹੋ ਸਕਦੀਆਂ ਹਨ; ਜਾਂ ਅਨੰਤਤਾ 'ਤੇ ਸ਼ੁਰੂ ਹੋ ਸਕਦੀਆਂ ਹਨ ਅਤੇ ਨੈਗੇਟਿਵ ਚਾਰਜਾਂ ਨਾਲ ਖਤਮ ਹੋ ਸਕਦੀਆਂ ਹਨ; ਜਾਂ ਬੰਦ ਲੂਪ ਬਣਾਉਂਦੀਆਂ ਹਨ ਜੋ ਨਾ ਤਾਂ ਕਿਸੇ ਚਾਰਜ ਨਾਲ ਸ਼ੁਰੂ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਨਾ ਹੀ ਖਤਮ ਹੁੰਦੀਆਂ ਹਨ। ਚੁੰਬਕੀ ਫੀਲਡ ਲਾਈਨਾਂ ਹਮੇਸ਼ਾ ਕਰੰਟ-ਲੈਣ ਵਾਲੇ ਕੰਡਕਟਰਾਂ ਦੇ ਦੁਆਲੇ ਬੰਦ ਲੂਪ ਬਣਾਉਂਦੀਆਂ ਹਨ ਕਿਉਂਕਿ ਭੌਤਿਕ ਵਿਗਿਆਨ ਵਿੱਚ ਕੋਈ ਚੁੰਬਕੀ ਚਾਰਜ ਨਹੀਂ ਹੁੰਦੇ। ਕੁਝ ਗਣਿਤਿਕ ਫਾਰਮੂਲਿਆਂ ਵਿੱਚ, ਬਰਾਬਰ ਚੁੰਬਕੀ ਚਾਰਜ ਅਤੇ ਚੁੰਬਕੀ ਕਰੰਟ ਸ਼ਕਤੀ ਅਤੇ ਚੁੰਬਕੀ ਸਰੋਤਾਂ ਨੂੰ ਸ਼ਾਮਲ ਕਰਨ ਵਾਲੇ ਹੱਲਾਂ ਵਿਚਕਾਰ ਦਵੈਤ ਦਿਖਾਉਣ ਲਈ ਪੇਸ਼ ਕੀਤੇ ਜਾਂਦੇ ਹਨ।
ਦੋ ਕੰਡਕਟਰਾਂ ਵਿਚਕਾਰ ਖਿੱਚੀਆਂ ਗਈਆਂ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ ਚਾਰਜ ਦੀ ਵੰਡ ਨੂੰ ਦਰਸਾਉਣ ਵਿੱਚ ਮਦਦ ਕਰਦੀਆਂ ਹਨ। ਜੇਕਰ ਅਸੀਂ ਇਹ ਮੰਨਦੇ ਹਾਂ ਕਿ ਵੋਲਟੇਜ ਸਰੋਤ ਸਾਈਨਸੌਇਡਲ ਹੈ, ਤਾਂ ਅਸੀਂ ਉਮੀਦ ਕਰਦੇ ਹਾਂ ਕਿ ਕੰਡਕਟਰਾਂ ਵਿਚਕਾਰ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਵੀ ਸਾਈਨਸੌਇਡਲ ਹੋਵੇਗਾ ਜਿਸਦਾ ਪੀਰੀਅਡ ਸਰੋਤ ਦੇ ਬਰਾਬਰ ਹੋਵੇਗਾ। ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਤਾਕਤ ਦੀ ਸਾਪੇਖਿਕ ਤੀਬਰਤਾ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ ਦੀ ਘਣਤਾ ਦੁਆਰਾ ਦਰਸਾਈ ਜਾਂਦੀ ਹੈ, ਅਤੇ ਤੀਰ ਸਾਪੇਖਿਕ ਦਿਸ਼ਾ (ਸਕਾਰਾਤਮਕ ਜਾਂ ਨਕਾਰਾਤਮਕ) ਨੂੰ ਦਰਸਾਉਂਦੇ ਹਨ। ਕੰਡਕਟਰਾਂ ਵਿਚਕਾਰ ਸਮੇਂ-ਸਮੇਂ 'ਤੇ ਬਦਲਦੇ ਇਲੈਕਟ੍ਰਿਕ ਅਤੇ ਚੁੰਬਕੀ ਖੇਤਰਾਂ ਦੀ ਉਤਪਤੀ ਇੱਕ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਤਰੰਗ ਬਣਾਉਂਦੀ ਹੈ ਜੋ ਟ੍ਰਾਂਸਮਿਸ਼ਨ ਲਾਈਨ ਦੇ ਨਾਲ ਫੈਲਦੀ ਹੈ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ 3(a) ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ। ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਤਰੰਗ ਚਾਰਜ ਅਤੇ ਸੰਬੰਧਿਤ ਕਰੰਟ ਦੇ ਨਾਲ ਐਂਟੀਨਾ ਵਿੱਚ ਦਾਖਲ ਹੁੰਦੀ ਹੈ। ਜੇਕਰ ਅਸੀਂ ਐਂਟੀਨਾ ਢਾਂਚੇ ਦੇ ਕੁਝ ਹਿੱਸੇ ਨੂੰ ਹਟਾਉਂਦੇ ਹਾਂ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ 3(b) ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ, ਤਾਂ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ ਦੇ ਖੁੱਲ੍ਹੇ ਸਿਰਿਆਂ ਨੂੰ "ਜੋੜ" ਕੇ ਇੱਕ ਫ੍ਰੀ-ਸਪੇਸ ਵੇਵ ਬਣਾਈ ਜਾ ਸਕਦੀ ਹੈ (ਬਿੰਦੀਆਂ ਵਾਲੀਆਂ ਲਾਈਨਾਂ ਦੁਆਰਾ ਦਿਖਾਇਆ ਗਿਆ ਹੈ)। ਫ੍ਰੀ-ਸਪੇਸ ਵੇਵ ਵੀ ਆਵਰਤੀ ਹੈ, ਪਰ ਸਥਿਰ-ਪੜਾਅ ਬਿੰਦੂ P0 ਪ੍ਰਕਾਸ਼ ਦੀ ਗਤੀ 'ਤੇ ਬਾਹਰ ਵੱਲ ਵਧਦਾ ਹੈ ਅਤੇ ਅੱਧੇ ਸਮੇਂ ਵਿੱਚ λ/2 (P1 ਤੱਕ) ਦੀ ਦੂਰੀ ਤੈਅ ਕਰਦਾ ਹੈ। ਐਂਟੀਨਾ ਦੇ ਨੇੜੇ, ਸਥਿਰ-ਪੜਾਅ ਬਿੰਦੂ P0 ਪ੍ਰਕਾਸ਼ ਦੀ ਗਤੀ ਨਾਲੋਂ ਤੇਜ਼ ਚਲਦਾ ਹੈ ਅਤੇ ਐਂਟੀਨਾ ਤੋਂ ਦੂਰ ਬਿੰਦੂਆਂ 'ਤੇ ਪ੍ਰਕਾਸ਼ ਦੀ ਗਤੀ ਦੇ ਨੇੜੇ ਆਉਂਦਾ ਹੈ। ਚਿੱਤਰ 4 t = 0, t/8, t/4, ਅਤੇ 3T/8 'ਤੇ λ∕2 ਐਂਟੀਨਾ ਦੀ ਖਾਲੀ-ਸਪੇਸ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਵੰਡ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ।
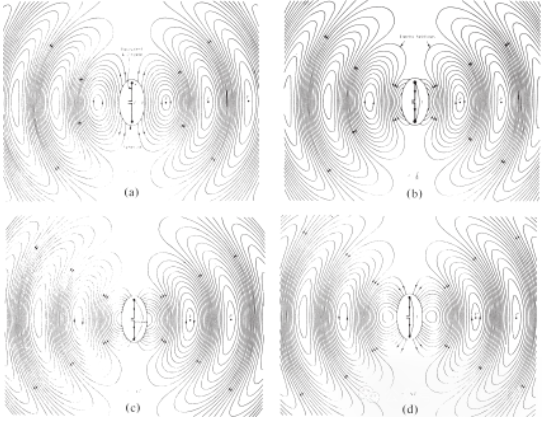
ਚਿੱਤਰ 4 t = 0, t/8, t/4 ਅਤੇ 3T/8 'ਤੇ λ∕2 ਐਂਟੀਨਾ ਦੀ ਖਾਲੀ ਥਾਂ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਵੰਡ
ਇਹ ਪਤਾ ਨਹੀਂ ਹੈ ਕਿ ਗਾਈਡਡ ਤਰੰਗਾਂ ਐਂਟੀਨਾ ਤੋਂ ਕਿਵੇਂ ਵੱਖ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਅੰਤ ਵਿੱਚ ਖਾਲੀ ਥਾਂ ਵਿੱਚ ਪ੍ਰਸਾਰਿਤ ਹੋਣ ਲਈ ਕਿਵੇਂ ਬਣਦੀਆਂ ਹਨ। ਅਸੀਂ ਗਾਈਡਡ ਅਤੇ ਖਾਲੀ ਥਾਂ ਤਰੰਗਾਂ ਦੀ ਤੁਲਨਾ ਪਾਣੀ ਦੀਆਂ ਤਰੰਗਾਂ ਨਾਲ ਕਰ ਸਕਦੇ ਹਾਂ, ਜੋ ਕਿ ਪਾਣੀ ਦੇ ਸ਼ਾਂਤ ਸਰੀਰ ਵਿੱਚ ਡਿੱਗੇ ਪੱਥਰ ਕਾਰਨ ਜਾਂ ਹੋਰ ਤਰੀਕਿਆਂ ਨਾਲ ਹੋ ਸਕਦੀਆਂ ਹਨ। ਇੱਕ ਵਾਰ ਪਾਣੀ ਵਿੱਚ ਗੜਬੜ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦੀ ਹੈ, ਤਾਂ ਪਾਣੀ ਦੀਆਂ ਤਰੰਗਾਂ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਬਾਹਰ ਵੱਲ ਫੈਲਣੀਆਂ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦੀਆਂ ਹਨ। ਭਾਵੇਂ ਗੜਬੜ ਰੁਕ ਜਾਵੇ, ਲਹਿਰਾਂ ਰੁਕਦੀਆਂ ਨਹੀਂ ਹਨ ਸਗੋਂ ਅੱਗੇ ਫੈਲਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ। ਜੇਕਰ ਗੜਬੜ ਜਾਰੀ ਰਹਿੰਦੀ ਹੈ, ਤਾਂ ਨਵੀਆਂ ਤਰੰਗਾਂ ਲਗਾਤਾਰ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ, ਅਤੇ ਇਹਨਾਂ ਤਰੰਗਾਂ ਦਾ ਪ੍ਰਸਾਰ ਦੂਜੀਆਂ ਤਰੰਗਾਂ ਤੋਂ ਪਿੱਛੇ ਰਹਿ ਜਾਂਦਾ ਹੈ।
ਇਹੀ ਗੱਲ ਬਿਜਲੀ ਦੇ ਗੜਬੜ ਦੁਆਰਾ ਪੈਦਾ ਹੋਣ ਵਾਲੀਆਂ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਤਰੰਗਾਂ ਲਈ ਵੀ ਸੱਚ ਹੈ। ਜੇਕਰ ਸਰੋਤ ਤੋਂ ਸ਼ੁਰੂਆਤੀ ਬਿਜਲੀ ਗੜਬੜ ਥੋੜ੍ਹੇ ਸਮੇਂ ਦੀ ਹੈ, ਤਾਂ ਪੈਦਾ ਹੋਈਆਂ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਤਰੰਗਾਂ ਟ੍ਰਾਂਸਮਿਸ਼ਨ ਲਾਈਨ ਦੇ ਅੰਦਰ ਫੈਲਦੀਆਂ ਹਨ, ਫਿਰ ਐਂਟੀਨਾ ਵਿੱਚ ਦਾਖਲ ਹੁੰਦੀਆਂ ਹਨ, ਅਤੇ ਅੰਤ ਵਿੱਚ ਖਾਲੀ ਸਪੇਸ ਤਰੰਗਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਰੇਡੀਏਟ ਹੁੰਦੀਆਂ ਹਨ, ਭਾਵੇਂ ਉਤੇਜਨਾ ਹੁਣ ਮੌਜੂਦ ਨਹੀਂ ਹੈ (ਬਿਲਕੁਲ ਪਾਣੀ ਦੀਆਂ ਤਰੰਗਾਂ ਅਤੇ ਉਹਨਾਂ ਦੁਆਰਾ ਪੈਦਾ ਕੀਤੀ ਗਈ ਗੜਬੜ ਵਾਂਗ)। ਜੇਕਰ ਬਿਜਲੀ ਗੜਬੜ ਨਿਰੰਤਰ ਹੈ, ਤਾਂ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਤਰੰਗਾਂ ਨਿਰੰਤਰ ਮੌਜੂਦ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਪ੍ਰਸਾਰ ਦੌਰਾਨ ਉਹਨਾਂ ਦੇ ਪਿੱਛੇ-ਪਿੱਛੇ ਚੱਲਦੀਆਂ ਹਨ, ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ 5 ਵਿੱਚ ਦਿਖਾਏ ਗਏ ਬਾਈਕੋਨਿਕਲ ਐਂਟੀਨਾ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ। ਜਦੋਂ ਇਲੈਕਟ੍ਰੋਮੈਗਨੈਟਿਕ ਤਰੰਗਾਂ ਟ੍ਰਾਂਸਮਿਸ਼ਨ ਲਾਈਨਾਂ ਅਤੇ ਐਂਟੀਨਾ ਦੇ ਅੰਦਰ ਹੁੰਦੀਆਂ ਹਨ, ਤਾਂ ਉਹਨਾਂ ਦੀ ਹੋਂਦ ਕੰਡਕਟਰ ਦੇ ਅੰਦਰ ਬਿਜਲੀ ਚਾਰਜ ਦੀ ਹੋਂਦ ਨਾਲ ਸਬੰਧਤ ਹੁੰਦੀ ਹੈ। ਹਾਲਾਂਕਿ, ਜਦੋਂ ਤਰੰਗਾਂ ਰੇਡੀਏਟ ਹੁੰਦੀਆਂ ਹਨ, ਤਾਂ ਉਹ ਇੱਕ ਬੰਦ ਲੂਪ ਬਣਾਉਂਦੀਆਂ ਹਨ ਅਤੇ ਉਹਨਾਂ ਦੀ ਹੋਂਦ ਨੂੰ ਬਣਾਈ ਰੱਖਣ ਲਈ ਕੋਈ ਚਾਰਜ ਨਹੀਂ ਹੁੰਦਾ। ਇਹ ਸਾਨੂੰ ਇਸ ਸਿੱਟੇ 'ਤੇ ਲੈ ਜਾਂਦਾ ਹੈ ਕਿ:
ਫੀਲਡ ਦੇ ਉਤੇਜਨਾ ਲਈ ਚਾਰਜ ਦੇ ਪ੍ਰਵੇਗ ਅਤੇ ਗਿਰਾਵਟ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ, ਪਰ ਫੀਲਡ ਦੇ ਰੱਖ-ਰਖਾਅ ਲਈ ਚਾਰਜ ਦੇ ਪ੍ਰਵੇਗ ਅਤੇ ਗਿਰਾਵਟ ਦੀ ਲੋੜ ਨਹੀਂ ਹੁੰਦੀ।
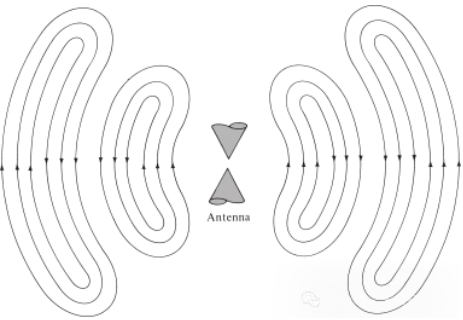
ਚਿੱਤਰ 5
3. ਡਾਇਪੋਲ ਰੇਡੀਏਸ਼ਨ
ਅਸੀਂ ਉਸ ਵਿਧੀ ਨੂੰ ਸਮਝਾਉਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੇ ਹਾਂ ਜਿਸ ਦੁਆਰਾ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ ਐਂਟੀਨਾ ਤੋਂ ਵੱਖ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਫ੍ਰੀ-ਸਪੇਸ ਤਰੰਗਾਂ ਬਣਾਉਂਦੀਆਂ ਹਨ, ਅਤੇ ਇੱਕ ਉਦਾਹਰਣ ਵਜੋਂ ਡਾਇਪੋਲ ਐਂਟੀਨਾ ਲੈਂਦੇ ਹਾਂ। ਹਾਲਾਂਕਿ ਇਹ ਇੱਕ ਸਰਲ ਵਿਆਖਿਆ ਹੈ, ਇਹ ਲੋਕਾਂ ਨੂੰ ਫ੍ਰੀ-ਸਪੇਸ ਤਰੰਗਾਂ ਦੇ ਉਤਪਾਦਨ ਨੂੰ ਸਹਿਜ ਰੂਪ ਵਿੱਚ ਦੇਖਣ ਦੇ ਯੋਗ ਵੀ ਬਣਾਉਂਦੀ ਹੈ। ਚਿੱਤਰ 6(a) ਚੱਕਰ ਦੀ ਪਹਿਲੀ ਤਿਮਾਹੀ ਵਿੱਚ ਜਦੋਂ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ λ∕4 ਦੁਆਰਾ ਬਾਹਰ ਵੱਲ ਵਧਦੀਆਂ ਹਨ ਤਾਂ ਡਾਇਪੋਲ ਦੀਆਂ ਦੋ ਬਾਹਾਂ ਵਿਚਕਾਰ ਪੈਦਾ ਹੋਈਆਂ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ। ਇਸ ਉਦਾਹਰਣ ਲਈ, ਆਓ ਇਹ ਮੰਨ ਲਈਏ ਕਿ ਬਣੀਆਂ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ ਦੀ ਗਿਣਤੀ 3 ਹੈ। ਚੱਕਰ ਦੀ ਅਗਲੀ ਤਿਮਾਹੀ ਵਿੱਚ, ਮੂਲ ਤਿੰਨ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ ਇੱਕ ਹੋਰ λ∕4 (ਸ਼ੁਰੂਆਤੀ ਬਿੰਦੂ ਤੋਂ ਕੁੱਲ λ∕2) ਨੂੰ ਹਿਲਾਉਂਦੀਆਂ ਹਨ, ਅਤੇ ਕੰਡਕਟਰ 'ਤੇ ਚਾਰਜ ਘਣਤਾ ਘਟਣੀ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦੀ ਹੈ। ਇਸਨੂੰ ਉਲਟ ਚਾਰਜਾਂ ਦੀ ਸ਼ੁਰੂਆਤ ਦੁਆਰਾ ਬਣਾਇਆ ਗਿਆ ਮੰਨਿਆ ਜਾ ਸਕਦਾ ਹੈ, ਜੋ ਚੱਕਰ ਦੇ ਪਹਿਲੇ ਅੱਧ ਦੇ ਅੰਤ ਵਿੱਚ ਕੰਡਕਟਰ 'ਤੇ ਚਾਰਜਾਂ ਨੂੰ ਰੱਦ ਕਰਦੇ ਹਨ। ਉਲਟ ਚਾਰਜਾਂ ਦੁਆਰਾ ਪੈਦਾ ਹੋਣ ਵਾਲੀਆਂ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ 3 ਹਨ ਅਤੇ λ∕4 ਦੀ ਦੂਰੀ ਤੈਅ ਕਰਦੀਆਂ ਹਨ, ਜਿਸਨੂੰ ਚਿੱਤਰ 6(b) ਵਿੱਚ ਬਿੰਦੀਆਂ ਵਾਲੀਆਂ ਲਾਈਨਾਂ ਦੁਆਰਾ ਦਰਸਾਇਆ ਗਿਆ ਹੈ।
ਅੰਤਮ ਨਤੀਜਾ ਇਹ ਹੈ ਕਿ ਪਹਿਲੀ λ∕4 ਦੂਰੀ ਵਿੱਚ ਤਿੰਨ ਹੇਠਾਂ ਵੱਲ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ ਹਨ ਅਤੇ ਦੂਜੀ λ∕4 ਦੂਰੀ ਵਿੱਚ ਉੱਪਰ ਵੱਲ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ ਦੀ ਇੱਕੋ ਜਿਹੀ ਗਿਣਤੀ ਹੈ। ਕਿਉਂਕਿ ਐਂਟੀਨਾ 'ਤੇ ਕੋਈ ਸ਼ੁੱਧ ਚਾਰਜ ਨਹੀਂ ਹੈ, ਇਸ ਲਈ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਲਾਈਨਾਂ ਨੂੰ ਕੰਡਕਟਰ ਤੋਂ ਵੱਖ ਹੋਣ ਅਤੇ ਇੱਕ ਬੰਦ ਲੂਪ ਬਣਾਉਣ ਲਈ ਇਕੱਠੇ ਜੁੜਨ ਲਈ ਮਜਬੂਰ ਕੀਤਾ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ। ਇਹ ਚਿੱਤਰ 6(c) ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ। ਦੂਜੇ ਅੱਧ ਵਿੱਚ, ਉਹੀ ਭੌਤਿਕ ਪ੍ਰਕਿਰਿਆ ਦੀ ਪਾਲਣਾ ਕੀਤੀ ਜਾਂਦੀ ਹੈ, ਪਰ ਧਿਆਨ ਦਿਓ ਕਿ ਦਿਸ਼ਾ ਉਲਟ ਹੈ। ਇਸ ਤੋਂ ਬਾਅਦ, ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਦੁਹਰਾਇਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਅਣਮਿੱਥੇ ਸਮੇਂ ਲਈ ਜਾਰੀ ਰਹਿੰਦਾ ਹੈ, ਚਿੱਤਰ 4 ਦੇ ਸਮਾਨ ਇੱਕ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਵੰਡ ਬਣਾਉਂਦਾ ਹੈ।
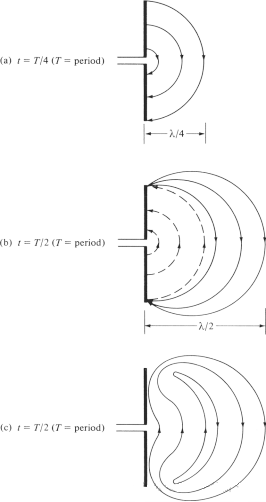
ਚਿੱਤਰ 6
ਐਂਟੀਨਾ ਬਾਰੇ ਹੋਰ ਜਾਣਨ ਲਈ, ਕਿਰਪਾ ਕਰਕੇ ਇੱਥੇ ਜਾਓ:
ਪੋਸਟ ਸਮਾਂ: ਜੂਨ-20-2024










