ਐਂਟੀਨਾ ਦੀ ਦੁਨੀਆ ਵਿੱਚ, ਇੱਕ ਅਜਿਹਾ ਕਾਨੂੰਨ ਹੈ। ਜਦੋਂ ਇੱਕ ਲੰਬਕਾਰੀਪੋਲਰਾਈਜ਼ਡ ਐਂਟੀਨਾਸੰਚਾਰਿਤ ਕਰਦਾ ਹੈ, ਇਸਨੂੰ ਸਿਰਫ਼ ਇੱਕ ਲੰਬਕਾਰੀ ਧਰੁਵੀਕ੍ਰਿਤ ਐਂਟੀਨਾ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ; ਜਦੋਂ ਇੱਕ ਖਿਤਿਜੀ ਧਰੁਵੀਕ੍ਰਿਤ ਐਂਟੀਨਾ ਸੰਚਾਰਿਤ ਕਰਦਾ ਹੈ, ਤਾਂ ਇਸਨੂੰ ਸਿਰਫ਼ ਇੱਕ ਖਿਤਿਜੀ ਧਰੁਵੀਕ੍ਰਿਤ ਐਂਟੀਨਾ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ; ਜਦੋਂ ਇੱਕ ਸੱਜੇ-ਹੱਥਗੋਲਾਕਾਰ ਧਰੁਵੀਕ੍ਰਿਤ ਐਂਟੀਨਾਸੰਚਾਰਿਤ ਕਰਦਾ ਹੈ, ਇਸਨੂੰ ਸਿਰਫ਼ ਸੱਜੇ-ਹੱਥ ਦੇ ਗੋਲਾਕਾਰ ਧਰੁਵੀਕਰਨ ਵਾਲੇ ਐਂਟੀਨਾ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ; ਜਦੋਂ ਇੱਕ ਖੱਬੇ-ਹੱਥ ਦਾ ਗੋਲਾਕਾਰ ਧਰੁਵੀਕਰਨ ਵਾਲਾ ਐਂਟੀਨਾ ਸੰਚਾਰਿਤ ਕਰਦਾ ਹੈ, ਤਾਂ ਇਸਨੂੰ ਸਿਰਫ਼ ਸੱਜੇ-ਹੱਥ ਦੇ ਗੋਲਾਕਾਰ ਧਰੁਵੀਕਰਨ ਵਾਲੇ ਐਂਟੀਨਾ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ; ਗੋਲਾਕਾਰ ਧਰੁਵੀਕਰਨ ਵਾਲਾ ਐਂਟੀਨਾ ਸੰਚਾਰਿਤ ਕਰਦਾ ਹੈ ਅਤੇ ਸਿਰਫ਼ ਖੱਬੇ-ਹੱਥ ਦੇ ਗੋਲਾਕਾਰ ਧਰੁਵੀਕਰਨ ਵਾਲੇ ਐਂਟੀਨਾ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ।
ਆਰ.ਐਫ.ਐਮ.ਐਸ.ਓ.ਗੋਲਾਕਾਰ ਪੋਲਰਾਈਜ਼ਡ ਹਾਰਨ ਐਂਟੀਨਾ ਉਤਪਾਦ
ਅਖੌਤੀ ਲੰਬਕਾਰੀ ਧਰੁਵੀਕਰਨ ਵਾਲਾ ਐਂਟੀਨਾ ਐਂਟੀਨਾ ਦੁਆਰਾ ਨਿਕਲਣ ਵਾਲੀ ਤਰੰਗ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ, ਅਤੇ ਇਸਦੀ ਧਰੁਵੀਕਰਨ ਦਿਸ਼ਾ ਲੰਬਕਾਰੀ ਹੈ।
ਤਰੰਗ ਦੀ ਧਰੁਵੀਕਰਨ ਦਿਸ਼ਾ ਇਲੈਕਟ੍ਰਿਕ ਫੀਲਡ ਵੈਕਟਰ ਦੀ ਦਿਸ਼ਾ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ।
ਇਸ ਲਈ, ਤਰੰਗ ਦੀ ਧਰੁਵੀਕਰਨ ਦਿਸ਼ਾ ਲੰਬਕਾਰੀ ਹੈ, ਜਿਸਦਾ ਅਰਥ ਹੈ ਕਿ ਬਿਜਲੀ ਖੇਤਰ ਵੈਕਟਰ ਦੀ ਦਿਸ਼ਾ ਲੰਬਕਾਰੀ ਹੈ।
ਇਸੇ ਤਰ੍ਹਾਂ, ਇੱਕ ਖਿਤਿਜੀ ਧਰੁਵੀ ਐਂਟੀਨਾ ਦਾ ਮਤਲਬ ਹੈ ਕਿ ਤਰੰਗਾਂ ਦੀ ਦਿਸ਼ਾ ਖਿਤਿਜੀ ਹੈ, ਜਿਸਦਾ ਮਤਲਬ ਹੈ ਕਿ ਇਸ ਦੁਆਰਾ ਛੱਡੀਆਂ ਗਈਆਂ ਤਰੰਗਾਂ ਦੀ ਬਿਜਲੀ ਖੇਤਰ ਦੀ ਦਿਸ਼ਾ ਧਰਤੀ ਦੇ ਸਮਾਨਾਂਤਰ ਹੈ।
ਲੰਬਕਾਰੀ ਧਰੁਵੀਕਰਨ ਅਤੇ ਖਿਤਿਜੀ ਧਰੁਵੀਕਰਨ ਦੋਵੇਂ ਤਰ੍ਹਾਂ ਦੇ ਰੇਖਿਕ ਧਰੁਵੀਕਰਨ ਹਨ।
ਅਖੌਤੀ ਰੇਖਿਕ ਧਰੁਵੀਕਰਨ ਤਰੰਗਾਂ ਦੇ ਧਰੁਵੀਕਰਨ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ, ਯਾਨੀ ਕਿ, ਬਿਜਲੀ ਖੇਤਰ ਦੀ ਦਿਸ਼ਾ ਇੱਕ ਸਥਿਰ ਦਿਸ਼ਾ ਵਿੱਚ ਇਸ਼ਾਰਾ ਕਰਦੀ ਹੈ। ਸਥਿਰ ਦਾ ਮਤਲਬ ਹੈ ਕਿ ਇਹ ਨਹੀਂ ਬਦਲੇਗਾ।
ਗੋਲਾਕਾਰ ਧਰੁਵੀਕ੍ਰਿਤ ਐਂਟੀਨਾ ਤਰੰਗ ਦੇ ਧਰੁਵੀਕਰਨ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ, ਯਾਨੀ ਕਿ ਬਿਜਲੀ ਖੇਤਰ ਦੀ ਦਿਸ਼ਾ, ਜੋ ਸਮੇਂ ਦੇ ਬਦਲਣ ਨਾਲ ਇੱਕ ਸਮਾਨ ਕੋਣੀ ਵੇਗ w 'ਤੇ ਘੁੰਮਦੀ ਹੈ।
ਤਾਂ ਖੱਬੇ-ਹੱਥ ਅਤੇ ਸੱਜੇ-ਹੱਥ ਦੇ ਗੋਲਾਕਾਰ ਧਰੁਵੀਕਰਨ ਨੂੰ ਕਿਵੇਂ ਨਿਰਧਾਰਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ?
ਜਵਾਬ ਤੁਹਾਡੇ ਹੱਥਾਂ ਨਾਲ ਹੈ।
ਦੋਵੇਂ ਹੱਥਾਂ ਨੂੰ ਬਾਹਰ ਕੱਢੋ, ਉਨ੍ਹਾਂ ਦੇ ਅੰਗੂਠੇ ਤਰੰਗ ਪ੍ਰਸਾਰ ਦੀ ਦਿਸ਼ਾ ਵੱਲ ਇਸ਼ਾਰਾ ਕਰਦੇ ਹੋਏ, ਅਤੇ ਫਿਰ ਦੇਖੋ ਕਿ ਕਿਸ ਹੱਥ ਦੀਆਂ ਝੁਕੀਆਂ ਉਂਗਲਾਂ ਧਰੁਵੀਕਰਨ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਘੁੰਮਦੀਆਂ ਹਨ।
ਜੇਕਰ ਸੱਜਾ ਹੱਥ ਇੱਕੋ ਜਿਹਾ ਹੈ, ਤਾਂ ਇਹ ਸੱਜੇ ਹੱਥ ਦਾ ਧਰੁਵੀਕਰਨ ਹੈ; ਜੇਕਰ ਖੱਬਾ ਹੱਥ ਇੱਕੋ ਜਿਹਾ ਹੈ, ਤਾਂ ਇਹ ਖੱਬੇ ਹੱਥ ਦਾ ਧਰੁਵੀਕਰਨ ਹੈ।
ਅੱਗੇ, ਮੈਂ ਤੁਹਾਨੂੰ ਸਮਝਾਉਣ ਲਈ ਫਾਰਮੂਲਿਆਂ ਦੀ ਵਰਤੋਂ ਕਰਾਂਗਾ। ਹੁਣ ਮੰਨ ਲਓ ਕਿ ਦੋ ਰੇਖਿਕ ਧਰੁਵੀਕ੍ਰਿਤ ਤਰੰਗਾਂ ਹਨ।
ਇੱਕ ਧਰੁਵੀਕਰਨ ਦਿਸ਼ਾ x ਦਿਸ਼ਾ ਹੈ ਅਤੇ ਐਪਲੀਟਿਊਡ E1 ਹੈ; ਇੱਕ ਧਰੁਵੀਕਰਨ ਦਿਸ਼ਾ y ਦਿਸ਼ਾ ਹੈ ਅਤੇ ਐਪਲੀਟਿਊਡ E2 ਹੈ; ਦੋਵੇਂ ਤਰੰਗਾਂ z ਦਿਸ਼ਾ ਦੇ ਨਾਲ-ਨਾਲ ਫੈਲਦੀਆਂ ਹਨ।
ਦੋ ਤਰੰਗਾਂ ਨੂੰ ਉੱਪਰ ਰੱਖਦੇ ਹੋਏ, ਕੁੱਲ ਬਿਜਲੀ ਖੇਤਰ ਇਹ ਹੈ:
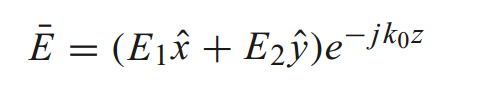
ਉਪਰੋਕਤ ਫਾਰਮੂਲੇ ਤੋਂ, ਬਹੁਤ ਸਾਰੀਆਂ ਸੰਭਾਵਨਾਵਾਂ ਹਨ:
(1) E1≠0, E2=0, ਫਿਰ ਸਮਤਲ ਤਰੰਗ ਦੀ ਧਰੁਵੀਕਰਨ ਦਿਸ਼ਾ x-ਧੁਰਾ ਹੈ
(2) E1=0, E2≠0, ਤਾਂ ਸਮਤਲ ਤਰੰਗ ਦੀ ਧਰੁਵੀਕਰਨ ਦਿਸ਼ਾ y-ਧੁਰਾ ਹੈ
(3) ਜੇਕਰ E1 ਅਤੇ E2 ਦੋਵੇਂ ਵਾਸਤਵਿਕ ਸੰਖਿਆਵਾਂ ਹਨ ਅਤੇ 0 ਨਹੀਂ ਹਨ, ਤਾਂ ਸਮਤਲ ਤਰੰਗ ਦੀ ਧਰੁਵੀਕਰਨ ਦਿਸ਼ਾ x-ਧੁਰੇ ਦੇ ਨਾਲ ਹੇਠ ਲਿਖੇ ਕੋਣ ਨੂੰ ਬਣਾਉਂਦੀ ਹੈ:
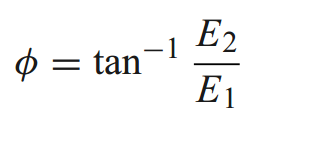
(4) ਜੇਕਰ E1 ਅਤੇ E2 ਵਿਚਕਾਰ ਇੱਕ ਖਾਸ ਪੜਾਅ ਅੰਤਰ ਹੈ, ਜਿਵੇਂ ਕਿ ਹੇਠਾਂ ਦਿੱਤੇ ਚਿੱਤਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ, ਤਾਂ ਸਮਤਲ ਤਰੰਗ ਇੱਕ ਸੱਜੇ-ਹੱਥ ਗੋਲਾਕਾਰ ਧਰੁਵੀਕਰਨ ਤਰੰਗ ਜਾਂ ਇੱਕ ਖੱਬੇ-ਹੱਥ ਗੋਲਾਕਾਰ ਧਰੁਵੀਕਰਨ ਤਰੰਗ ਬਣ ਸਕਦੀ ਹੈ।
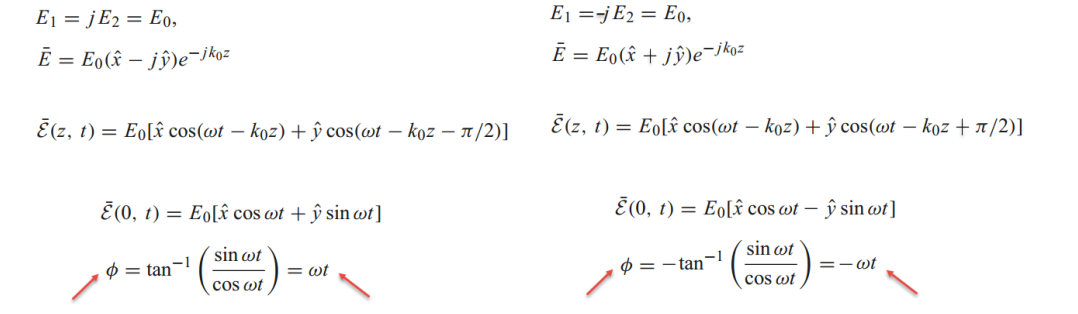
ਲੰਬਕਾਰੀ ਧਰੁਵੀਕ੍ਰਿਤ ਐਂਟੀਨਾ ਲਈ ਲੰਬਕਾਰੀ ਧਰੁਵੀਕ੍ਰਿਤ ਤਰੰਗਾਂ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ, ਅਤੇ ਖਿਤਿਜੀ ਧਰੁਵੀਕ੍ਰਿਤ ਐਂਟੀਨਾ ਲਈ ਖਿਤਿਜੀ ਧਰੁਵੀਕ੍ਰਿਤ ਤਰੰਗਾਂ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ, ਤੁਸੀਂ ਹੇਠਾਂ ਦਿੱਤੇ ਚਿੱਤਰ ਨੂੰ ਦੇਖ ਕੇ ਇਸਨੂੰ ਸਮਝ ਸਕਦੇ ਹੋ।
ਪਰ ਗੋਲਾਕਾਰ ਧਰੁਵੀਕਰਨ ਵਾਲੀਆਂ ਤਰੰਗਾਂ ਬਾਰੇ ਕੀ? ਗੋਲਾਕਾਰ ਧਰੁਵੀਕਰਨ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਵਿੱਚ, ਇਹ ਪੜਾਅ ਅੰਤਰਾਂ ਵਾਲੇ ਦੋ ਰੇਖਿਕ ਧਰੁਵੀਕਰਨਾਂ ਨੂੰ ਸੁਪਰਪੋਜ਼ ਕਰਕੇ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ।
ਐਂਟੀਨਾ ਬਾਰੇ ਹੋਰ ਜਾਣਨ ਲਈ, ਕਿਰਪਾ ਕਰਕੇ ਇੱਥੇ ਜਾਓ:
ਪੋਸਟ ਸਮਾਂ: ਮਈ-21-2024











